AVL tree vs RB tree with applications

 

AVL tree vs RB tree with applications

 

What is AVL Tree?

In 1962, GM Adelson - Velsky and EM Landis invented the AVL Tree. The tree is named AVL after its creators.

The AVL Tree is a height balanced binary search tree in which each node has a balance factor that is calculated by subtracting the height of its right sub-tree from the height of its left sub-tree.

If the balance factor of each node is between -1 and 1, the tree is said to be balanced; otherwise, the tree is unbalanced and must be balanced.

Balance Factor (k) = height (left(k)) - height (right(k))

If balance factor of any node is 1, it means that the left sub-tree is one level higher than the right sub-tree.

If balance factor of any node is 0, it means that the left sub-tree and right sub-tree contain equal height.

If balance factor of any node is -1, it means that the left sub-tree is one level lower than the right sub-tree.

The figure below depicts an AVL tree. We can see that the balance factor for each node is between -1 and +1. As a result, it is an example of an AVL tree.

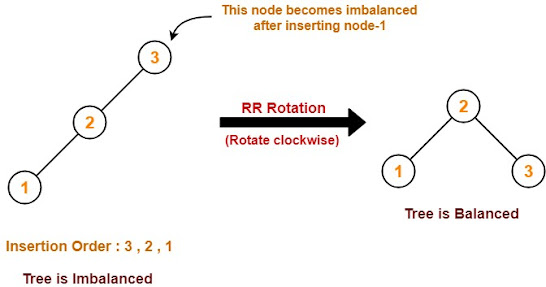
AVL Rotations:

If the balancing factor is not -1,1,0, it will balance itself by rotating. An AVL tree can balance itself by performing the four rotations listed below.

• Left rotation
• Right rotation
• Left-Right rotation
• Right-Left rotation

The first two rotations are single rotations, followed by double rotations. A tree of at least height 2 is required to have an unbalanced tree. Let's break them down one by one using this simple tree.

Case-01:

 

Case-02:

 

 

Case-03:

 

Case-04:

 

 

What is RB Tree?

A self-balancing binary search tree with a Red Black Tree is a type of self-balancing binary search tree. Rudolf Bayer invented it in 1972 and dubbed it "symmetric binary B-trees."

A red-black tree is a Binary tree in which each node has a color attribute, either red or black. By inspecting the node colors on any simple path from the root to a leaf, red-black trees ensure that no such path is more than twice as long as any other, ensuring the tree's overall balance.

Properties of Red-Black Trees:

A red-black tree is a binary search tree which has the following red-black properties:

All nodes are either red or black. Every (NULL) leaf is black. When a node is red, both of its children are black. There are the same number of black nodes on every simple path from a node to a descendant leaf. One of the most important characteristics of the Red-Black tree is that each leaf node should have the same black depth.                   A basic red-black tree:         Basic red-black tree with the nodes added:

 

 

 

Differences between the Red-Black tree and AVL tree:

1. Searching-

Because Red Black Trees are roughly balanced, they do not provide efficient searching. AVL trees, on the other hand, provide efficient searching because they are strictly balanced trees.

 

2. Insertion and Deletion -

 Insertion and deletion are simple because only a few rotations are required to balance the tree in insertion or deletion, whereas Insertion and Deletion are complex in the AVL tree because multiple rotations are required to balance the tree.

3. Node color-

 We color the nodes of the red black tree either red or black, but no color is required in the AVL tree.

4. Balance factor-

It does not contain any balance factor. It stores only one bit of information that denotes either Red or Black colour of the node whereas in AVL each node has a balance factor whose value can be 1, 0, or -1. It requires extra space to store the balance factor per node.

5.Strictly Balanced-

Red-black trees are not strictly balanced but AVL trees are strictly balanced, i.e., the left subtree's height and the height of the right subtree differ by at most 1.

 

6.Tools used for balancing trees-

If the tree is not balanced, then two tools are used for balancing the tree in a Red-Black tree:

1.       Recoloring

2.       Rotation

If the tree is not balanced, then one tool is used for balancing the tree in the AVL tree:

1.       Rotation

 Application:

1.  AVL TREES:

 

1.     AVL trees are mostly used for in-memory sorts of sets and dictionaries.

2.     AVL trees are also used extensively in database applications in which insertions and deletions are fewer but there are frequent lookups for data required.

3.     It is used in applications that require improved searching apart from the database applications.

 

2.  RB TREES:

1.     Most of the self-balancing BST library functions like map and set in C++ use Red-Black Tree.

2.     It is used to implement CPU Scheduling Linux. Completely Fair Scheduler uses it.

3.     Besides they are used in the K-mean clustering algorithm for reducing time complexity.

4.     Moreover, MySQL also uses the Red-Black tree for indexes on tables.

Conclusion:

In the case of the Red-Black tree, the insertion and deletion operations are efficient. If the tree gets balanced through the recoloring, then insertion and deletion operations are efficient in the Red-Black tree.

In the case of the AVL tree, the searching operation is efficient as it requires only one tool to balance the tree.